• Home
• Notazione
• Metodi Risolutivi
• Formule Risolutive
• Teoria
• Leggi del cubo
• Il Numero di Dio
• Conta Configurazioni Cubo
• Strategie Risolutive
• Genesi delle Formule
• Miscellaneous

Genesi delle formule risolutive

Cone si fa' a trovare una formula risolutiva??

In questa pagina voglio semplicemente proporre qualche idea a riguardo illustrando le tecniche da utilizzare.
Questo argomento è puramente teorico; in effetti non abbiamo alcun motivo di trovarne di nuove, in quanto probabilmente di nuove particolarmente efficienti non ce ne sono più da trovare; quello che a volte occorre fare per una certa formula è semplicemente trovare l'espressione che preferiamo eseguire utilizzando simmetrie, traslazioni o inversioni della formula che vogliamo adottare.

Nel seguito considererò unicamente formule che si applicano interamente su un solo strato del cubo; ossia le formule che normalmente si utilizzano nella realizzazione dell'ultimo strato di un qualunque metodo a strati ma tutte le considerazioni possono immediatamente essere estese a formule che interessano diversi strati del cubo utilizzate in altri metodi.

Premessa

Ho potuto individuare e formalizzare due diverse metodologie che riescono a spiegare l'origine di alcune formule: le due tecniche della coniugazione e del commutatore spiegate nella pagina sono in effetti le due tecniche base con cui si ottengono gli algoritmi risolutivi, nel cubo magico e in molti altri puzzles, tecniche comunque già ampiamente descritte da altri prima di me.
Per molte formule non ho ancora trovato alcun metodo e non saprei dire se queste siano le uniche tecniche utilizzabili e se tutte le formule risolutive siano ottenibili da una loro qualche composizione o se invece esistono altre tecniche, e nemmeno so' se per ogni formula sia in effetti possibile determinare una tecnica di formazione.
Le formule di cui riesco a spiegare la genesi sono sempre basate su di una sequenza base e su una sua alterazione secondo una o entrambe le due tecniche.

La sequenza base è una sequenza di mosse tale che muova un limitato numero di pezzi lasciando,una volta terminata la sequenza, tutti gli altri pezzi nelle loro originali posizioni.
Si potrebbe pensare la sequenza base come la generatrice della formula.
In generale opererà doppi scambi (tra due coppie di pezzi) e/o permutazioni tra tre pezzi o semplici orientamenti di due o tre pezzi (che sono i più semplici movimenti atomici consentiti dalla fisica del cubo).
Una sequenza base agirà in generale su pezzi disposti su differenti facce del cubo.
Quelle che ho potuto trovare sono tutte molto semplici, ma evidentemente potrebbero esistere sequenze base più complesse anche se non molto più lunghe, dato che solitamente le formule sono complessivamente lunghe meno di 16 mosse.

Come sequenza base si può utilizzare una ripetizione di una data sequenza base; la nuova formula ottenuta viene indicata con double o triple, alludendo al numero di volte che viene ripetuta la sequenza base (vedi per esempio Sune, Double Sune e Triple Sune).
Al momento ho determinato le seguenti Sequenze Base:

M2 U2 M2 U2
M' U2 M U2

U' R' U R
(U' R' U R)*3
(U R U' R')
(U R U' R')*2
(R U R' U')

R' D2 R

R' F' R U


ovviamente U R U' R', R U R' U' (inversa), U' R' U R (simmetrica) e R' U' R U (simmetrica inversa) sono fra loro equivalenti, nel senso che determinano la stessa tipologia di movimenti tra i pezzi solo cambiando i versi di rotazione e di permutazione.


L'aspetto essenziale da esaminare in una sequenza base è l'insieme dei pezzi interessati da questa, cioé l'insieme di spigoli ed angoli che una volta terminata la sequenza risultano modificati nella posizione o nell'orientamento, e che saranno in genere in numero piuttosto ridotto; dalla loro osservazione possono poi scaturire le idee per ottenere delle formule utili.

Una importante sequenza base che si sfrutta è la U R U' R' e le equivalenti simmetriche ed inverse ed opera lo scambio di due coppie di angoli e la permutazione di tre spigoli

Metodo della coniugazione (conjugation)

Questo metodo si basa sul ritrovamento di una sequenza base e sulla definizione della coniugazione e della relativa anticoniugazione che consentano di ottenere una formula.
Scopo della coniugazione è quello di portare in tutte le posizioni sensibili, che cioé risultino bersaglio della sequenza base considerata, pezzi appartenenti esclusivamente all'ultimo strato; scopo dell'anticoniugazione è ovviamente quello di ripristinare il corretto posizionamento ripercorrendo al contrario le mosse eseguite nella coniugazione; si tratta cioè di eseguire l'inversa della precedente coniugazione.

Formalmente:
(Coniugazione) (Sequenza Base) (Anticoniugazione)

Se indichiamo con C la Coniugazione e con X la Sequenza Base la tecnica della coniugazione si esprime con:
C X C'

M2 U M2 U2 M2 U M2
Azione: Scambio di due coppie di spigoli opposti senza alterarne l'orientamento

Sequenza base: M2 U2 M2 U2

La sequenza base esegue un doppio scambio di due spigoli, agendo sulle due coppie in posizione (UF, UB) e (DF, DB)
si tratta quindi di portare nelle posizioni DF e DB gli altri due spigoli che si trovano sulla faccia Up: UR e UL.
trovarla non è difficile.
Coniugazione: M2 U
in conseguenza resta definita l'anticoniugazione da eseguire
Anticoniugazione: U' M2

quindi concatenando le tre sequenze si ottiene
M2 U + M2 U2 M2 U2 + U' M2 = M2 U M2 U2 M2 U2 U' M2 = M2 U M2 U2 M2 U M2

M2 U M' U2 M2 U2 M' U' M2
Azione: Scambio di due coppie di spigoli adiacenti senza cambiarne l'orientamento

Sequenza base: M2 U2 M2 U2

Dalla formula precedente si osservi che una volta eseguita la coniugazione i 4 spigoli che prima erano sull'ultimo strato sono ora tutti nello strato M e che con la sequenza base si scambiano tra loro i due spigoli sulla faccia Up e i due spigoli sulla Down; eseguendo allora una ulteriore mossa M' lo scambio avverrà tra le due coppie di spigoli (UF, UL) e (UB, UR); quindi

Coniugazione: M2 U M
in conseguenza resta definita l'anticoniugazione da eseguire
Anticoniugazione: M' U' M2

e componendo le tre sequenze si ottiene
M2 U M + M2 U2 M2 U2 + M' U' M2 = M2 U M' U2 M2 U2 M' U' M2

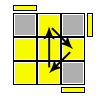
Sune: R U R' U R U2 R'
Nella genesi di questa formula considero solo la Sune propriamente detta:
R U R' U R U2 R'
Azione: Vedi anche queste altre spiegazioni sulla Sune

Sequenza base: U' R' U R

La sequenza base esegue un doppio scambio di due angoli, scambiando le due coppie in posizione (ULF, URF) e (URB, DRB) e permutando i tre spigoli UF, UR e BR.
La coniugazione da eseguire che consente di portare nelle posizioni attive della sequenza base tutti i pezzi dell'ultimo strato è una bella trovata.

Coniugazione: R U2
da cui
Anti coniugazione: U2 R'

Componendo le tre sequenze si ottiene:

R U2 + U' R' U R + U2 R' = R U2 U' R' U R U2 R' = R U R' U R U2 R

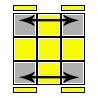
F (U R U' R')*3 F'
Azione: Scambio di due coppie di angoli adiacenti (come effetto secondario altera anche l'orientamento dei 4 angoli)

Sequenza base: (U R U' R')*3

Questa formula è una delle più semplici da capire in quanto la sequenza base e probabilmente la più semplice e naturale che esista e la coniugazione è molto semplice; la cosa interessante che si ottiene eseguendo la sequenza base 3 volte è che gli spigoli tornano al loro posto. Risulteranno scambiate le due coppie di angoli (URF, ULF) e (URB, ULB)
quindi è immediato trovare la coniugazione da eseguire

Coniugazione: F
da cui
Anti coniugazione: F'

Componendo le tre sequenze si ottiene:

F + (U R U' R')*3 + F' = F (U R U' R')*3 F'

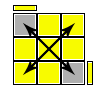
L' D2 (U R U' R')*3 D2 L
Azione: Scambio di due coppie di angoli opposti (come effetto secondario altera anche l'orientamento di 2 angoli)

Sequenza base: (U R U' R')*3

Si ripete esattamente il discorso della formula precedente ma eseguendo una diversa coniugazione

Coniugazione: L' D2
da cui
Anti coniugazione: D2 L

Componendo le tre sequenze si ottiene:

L' D2 + (U R U' R')*3 + D2 L' = L' D2 (U R U' R')*3 D2 L'

M U M' U2 M U M'
Azione: Permutazione oraria di tre spigoli col ribaltamento di due di questi

Sequenza base: M' U2 M U2

Questa sequenza base viene utilizzata come formula nel metodo corners first per permutare tre spigoli che si trovano nello strato M (UF, UB e DF); evidentemente sarà sufficiente trovare la coniugazione che posizioni nelle tre posizioni sensibili tre spigoli dell'ultimo strato; la coniugazione da usare è

Coniugazione: M U
da cui
Anti coniugazione: U' M'

[Coniugazione per la simmetrica: M U']

Componendo le tre sequenze si ottiene:

M U + M' U2 M U2 + U' M' = M U M' U2 M U2 U' M' = M U M' U2 M U M'

Allan: F2 U M' U2 M U F2
Azione: Permutazione oraria di tre spigoli senza alterarne l'orientamento

Sequenza base: M' U2 M U2

Si tratta della stessa sequenza base precedente ma con una diversa coniugazione per portare nelle tre posizioni target tre spigoli dell'ultimo strato;

Coniugazione: F2 U
Anti coniugazione: U' F2

[Coniugazione per Allan simmetrica: F2 U']

Componendo le tre sequenze si ottiene:

F2 U + M' U2 M U2 + U' F2 = F2 U M' U2 M U2 U' F2 = F2 U M' U2 M U F2

Metodo del commutatore (commutator)

Ho adottato la denominazione di tale metodo da un paio di siti inglesi dove ne accennavano chiamandolo così (commutator).
Il metodo del commutatore che chiamerei anche metodo della sostituzione consiste nell'eseguire una semplice sequenza base, sostituire un pezzo con un altro, ripercorrere all'indietro la sequenza base cioè eseguire la sequenza base inversa (o anti sequenza base se preferite) ed infine ritornare indietro anche con la mossa (o le mosse) di sostituzione eseguendone l'inversa.
Sostituire un pezzo significa eseguire una o più mosse che mi consentano di andare a sostituire uno dei pezzi coinvolti dalla sequenza base con un altro pezzo non interessato dalla sequenza base; naturalmente entrambi i pezzi devono appartenere all'ultimo strato dal momento che sto' esaminando solo formule che siano da utilizzare nella risoluzione del terzo strato; ripercorrendo al contrario la sequenza base lo scambio avverrà tra uno dei due pezzi precedenti ed un nuovo pezzo, il che provocherà una permutazione di tre pezzi (3-cycle permutation).
Quindi in generale le formule ottenute col commutatore realizzano una permutazione di tre pezzi (3-cycle perm).

Formalmente:
(Sequenza base) (Sostituzione) (Sequenza base inversa) (Sostituzione inversa)

Si deve ora osservare che non c'è nessuna differenza tra la sequenza base e la sostituzione nel senso che sono entrambe due generiche sequenze di mosse che differenzio esclusivamente a livello di logica; la sequenza base è normalmente una breve formula di tre o quattro mosse mentre la sostituzione consiste di una o due mosse; più in generale si può allora considerare la concatenazione di due generiche sequenze di mosse secondo lo schema X Y X' Y' entrambe composte da più mosse e come caso particolare di questa genealizzazione si può allora arrivare ad uno schema del tipo:
(Sostituzione) (Sequenza base) (Sostituzione inversa) (Sequenza base inversa)
in cui la sostituzione preceda la sequenza base anziché seguirla.

Scambiando l'ordine della sequenza base e della sostituzione si ottiene la medesima permutazione ma in verso contrario.
Più precisamente se chiamiamo X la Sostituzione e Y la Sequenza Base (o viceversa) si osserva che la tecnica del permutatore si esprime con:
X Y X' Y'
scambiando la sostituzione e la sequenza base (cioé applicando prima la Sequenza Base e poi la Sostituzione) si ottiene:
Y X Y' X'
Si può allora osservare che lo scambio tra X ed Y porta ad ottenere la formula inversa che darà quindi una permutazione in verso contrario; infatti l'inversa di X Y X' Y' è data da (X Y X' Y')' = Y X Y' X'.

U + Niklas: (U) R U' L' U R' U' L
Azione: Permutazione di tre angoli in senso orario dandogli spin +1/3
Per ulteriori considerazioni su tale formula guarda anche queste spiegazioni sulla Niklas

Sequenza base: U R U' R'
Sequenza base inversa: R U R' U'


La sequenza base esegue un doppio scambio di due angoli, scambiando le due coppie in posizione (ULB, URB) e (URF, DRF) e permutando i tre spigoli UB, UR e FR
eseguita questa sequenza base si nota che l'angolo in ULB è l'unico pezzo coinvolto dalla sequenza base che si trovi sulla faccia left; se allora si esegue la sostituzione noi sostituiamo quel pezzo (che è l'angolo che che proviene dalla posizione URB) con l'angolo ULF; rieseguendo la sequenza base al contrario si scambieranno nuovamente i pezzi nelle posizioni (ULB, URB) i quali ora sono i pezzi provenienti dalle posizioni URB e ULF; eseguendo infine la sostituzione inversa otterremo la permutazione di tre angoli.
in conseguenza resta definita l'anticoniugazione da eseguire.

Sostituzione: L'
Sostituzione Inversa: L

quindi concatenando le quattro sequenze si ottiene:

U R U' R' + L' + R U R' U' + L = U R U' L' U R' U' L

Double Niklas: (U R U' R')*2 L' (R U R' U')*2 L
Azione: Orientamento di due angoli, uno con spin +1/3 ed uno con spin -1/3

Sequenza base: (U R U' R')*2
Sequenza base inversa: (R U R' U')*2

Eseguendo la sequenza base U R U' R' per 2 volte si nota che gli angoli tornano al loro posto ma orientati diversamente; questo fornisce lo spunto per provare una sostituzione di quel solo angolo; dopo la sostituzione eseguendo la sequenza base inversa si orienterà in verso opposto un altro angolo.

Sostituzione: L'
Sostituzione Inversa: L

quindi concatenando le quattro sequenze si ottiene:
(U R U' R')*2 + L' + (R U R' U')*2 + L = (U R U' R')*2 L' (R U R' U')*2 L

Siccome la sequenza base viene eseguita due volte ho chiamato questa formula Double Niklas in analogia con quanto avviene per Sune e Double Sune. Tuttavia si tenga presente che la Double Niklas utilizza la (U + Niklas) e non la sola Niklas e soprattutto la Sune viene realizzata con la coniugazione mentre la Niklas col commutatore.

R U R' U' Rw R' U R U' Rw'
Azione: Permutazione di tre spigoli in senso antiorario ribaltandone due.
Utilizzata nell'OLL del Fridrich.
L'espressione della formula utilizzando la notazione Rw la rende molto bella da eseguirsi ma anche oscura rispetto alla sua genesi; occorre quindi rifarsi ad una espressione della stessa formula che non utilizzi la Rw.
Osservando che M = Rw R' [vedi pagina notazioni] e anche Rw = R M e anche Rw' = R' M' [senza starsi a fare troppe domande sull'agebra utilizzata basta verificarlo empiricamente]

R U R' U' Rw R' U R U' Rw' = (R U R' U') Rw R' (U R U' Rw') = (R U R' U') M' (U R U' R' M) = (R U R' U') M' (U R U' R' M)

quindi la formula in questione si può esprimere con

(R U R' U') M' (U R U' R') M

da cui si evince che

Sequenza base: R U R' U'
Sequenza base inversa: U R U' R'

Sostituzione: M'
Sostituzione Inversa: M

e la formula si ottiene componendo
(Sequenza base) (Sostituzione) (Sequenza base inversa) (Sostituzione inversa)

Evelyn inversa: Rw U R' U' L' U R U' x'
Azione: Permutazione di tre angoli in senso antiorario dando a due di questi uno spin di +1/3 e -1/3.
Utilizzata nell'OLL del Fridrich per orientare due angoli prima del posizionamento dei pezzi e nel metodo Petrus.
Può anche essere utilizzata per permutare tre angoli non ancora orientati senza interessare gli spigoli.


Il nome alla formula è stato assegnato da Lars Petrus.
Anche l'espressione di questa formula è scritta per ottenere una semplice e veloce esecuzione ma per comprenderne la genesi occorre elaborarne l'espressione in una forma più semplice da leggere.
Osservando che Rw = M R e anche Rw x = L' e anche x' = R' L M' [vedi pagina notazione] ed osservando che (M espressione M') = espressione in quanto questa espressione non agisce sui pezzi dello strato M

Rw U R' U' L' U R U' x' = (Rw) U R' U' (L') U R U' (x') = (M' R) U R' U' (L') U R U' (R' L M) = M' (R U R' U') L' (U R U' R') L M = (R U R' U') L' (U R U' R') L


quindi la Evelyn inversa si può esprimere con

(R U R' U') L' (U R U' R') L

da cui si evince che

Sequenza base: R U R' U'
Sequenza base inversa: U R U' R'

Sostituzione: L'
Sostituzione Inversa: L

e la formula si ottiene componendo
(Sequenza base) (Sostituzione) (Sequenza base inversa) (Sostituzione inversa)

T shape: R (U R') U' (R' F) (R F') = R (U R') U' (Lw' U) (R U') x'

Azione: utilizzata nell'OLL del Fridrich per risolvere una delle due configurazioni a T.
La formula risulta la somma delle due precedenti formule e complessivamente smuove parecchi pezzi e quindi non è troppo utile in metodi che non contengano un gran numero di formule; è però una formula da utilizzare per il solo orientamento dei pezzi nell'OLL del Fridrich.

Dall'osservazione delle due precedenti formule si potrebbe pensare di utilizzare la stessa sequenza base e come sostituzione l'unione delle due precedenti sostituzioni: M' + L' = Lw'

Sequenza base: R U R' U'
Sequenza base inversa: U R U' R'

Sostituzione: Lw'
Sostituzione Inversa: Lw


Infatti da (R U R' U') Lw' (U R U' R') Lw essendo R' Lw = x' si ottiene la formula.

Metodi composti

Si potrebbe pensare di realizzare una formula utilizzando in qualche modo entrambi i metodi descritti in precedenza.
Formalmente un semplice esempio di tale composizione potrebbe essere:
(Coniugazione) [(Sequenza) (Sostituzione) (Sequenza inversa) (Sostituzione inversa)] (Anti Coniugazione)
oppure
(Coniugazione) [(Sostituzione) (Sequenza base) (Sostituzione inversa) (Sequenza base inversa)] (Anti Coniugazione)

Si noti che scambiando l'ordine della sequenza e della sostituzione si ottiene la permutazione inversa (e quindi permuta ed orienta i pezzi in verso contrario)

Le parentesi hanno il solo scopo di chiarire la suddivisione logica.

Se indichiamo con C una coniugazione con S la Sostituzione e X la Sequenza Base la tecnica composta (la sola che al momento sono riuscito a determinare) si esprime con:
C S X S' X' C'


Esiste una rappresentazione formale compatta di tali operatori proposta da Lucas Garron.
Definiamo tre arbitrarie sequenze di mosse X, Y e Z
definiamo con X' Y' e Z' le inverse delle sequenze date e definiamo gli operatori virgola, punto e virgola e due punti:

[X: Y] rappresenta la sequenza X Y X' eseguita per prima nell'algoritmo
[X; Y] rappresenta la sequenza X Y X' eseguita per ultima nell'algoritmo
[X, Y] rappresenta la sequenza X Y X' Y'

dove gli operatori hanno un assegnato ordine di precedenza che dal primo all'ultimo è:
due punti, virgola, punto e virgola;
le parentesi definiscono l'intero algoritmo

quindi per esempio [X; Y, Z] rappresenta X (Y Z Y' Z') X'

Perfect Sequence Dx: Lw2 U R' D2 R U' R' D2 Lw' x = R2 D R' U2 R D' R' U2 R'

Azione: Permuta tra angoli orientandone due con spin opposti.
Utilizzata nell'OLL del Fridrich e nel metodo Petrus.

Occorre semplificare l'espressione della formula per renderla più comprensibile; i passaggi si basano sul fatto che Lw' x = R M2 L2 e sulla semplificazione M2 (espressione) M2 = (espressione) in quanto l'espressione in questione non interessa i pezzi dello strato M;
Lw2 U R' D2 R U' R' D2 Lw' x = (Lw2) U (R' D2 R) U' R' D2 (Lw' x) = (M2 L2) U (R' D2 R) U' R' D2 (R M2 L2) = M2 ( L2) U (R' D2 R) U' R' D2 (R L2) M2 = M2 L2 [U (R' D2 R) U' (R' D2 R)] L2 M2 = L2 [U (R' D2 R) U' (R' D2 R)] L2
Quindi la formula è anche uguale a:
L2 [U (R' D2 R) U' (R' D2 R)] L2


Sequenza base: R' D2 R
Sequenza base inversa: R' D2 R

Sostituzione: U
Sostituzione Inversa: U'

Coniugazione: L2
Anti Coniugazione: L2

da cui concatenando le varie espressioni:

(Coniugazione) + (Sostituzione) + (Sequenza base) + (Sostituzione inversa) + (Sequenza base inversa) + (Anti Coniugazione) = L2 + U + (R' D2 R) + U' + (R' D2 R) + L2

Lw' U R' D2 R U' R' D2 R2 x'

Azione: Permuta tra angoli senza alterarne l'orientamento (3-cycle clockwise corners permutation).
Utilizzata nel PLL del Fridrich.

Occorre semplificare l'espressione della formula per renderla più comprensibile; i passaggi si basano sul fatto che Lw' = M' L', R x' = L M Le sulla semplificazione M (espressione) M = (espressione) in quanto l'espressione in questione non interessa i pezzi dello strato M;
Lw' U R' D2 R U' R' D2 R2 x' = (Lw') U (R' D2 R) U' R' D2 (R2 x') = (M' L') U (R' D2 R) U' R' D2 (R L M) = M' L' U (R' D2 R) U' (R' D2 (R) L M = L' [U (R' D2 R) U' (R' D2 (R)] L
Quindi la formula è anche uguale a:
L' [U (R' D2 R) U' (R' D2 R)] L

Sequenza base: R' D2 R
Sequenza base inversa: R' D2 R

Sostituzione: U
Sostituzione Inversa: U'

Coniugazione: L'
Anti Coniugazione: L

da cui concatenando le varie espressioni:

(Coniugazione) + (Sostituzione) + (Sequenza) + (Sostituzione inversa) + (Sequenza inversa) + (Anti Coniugazione) = L' + U + (R' D2 R) + U' + (R' D2 R) + L


Scambiando l'ordine della Sequenza Base e della Sostituzione si ottiene la stessa permutazione in verso contrario:
(Coniugazione) + (Sequenza base) + (Sostituzione) + (Sequenza base inversa) + (Sostituzione inversa) + (Anti Coniugazione) = L' + (R' D2 R) + U + (R' D2 R) + U' + L

J Perm: R (U R') (F' R) (U R') U' (R' F) (R2 U') R' U' =

Azione: Scambia una coppia di angoli ed una coppia di spigoli senza alterarne l'orientamento
Utilizzata nel PLL del Fridrich

Sequenza base: R' F' R U
Sequenza base inversa: U' R' F R

Sostituzione: R'
Sostituzione Inversa: R

Coniugazione: R U
Anti Coniugazione: U' R'

Chiusura: U'

da cui concatenando le varie espressioni secondo lo schema:
Coniugazione + Sostituzione + Sequenza Base + Sostituzione inversa + Sequenza Base Inversa + Anti Coniugazione + Chiusura
si ottiene:
R U + R' F' R U + R' + U' R' F R + R + U' R' + U' = R U (R' F' R U) R' (U' R' F R) R U' R' (U')

Un secondo metodo composto si definisce semplicemente eseguendo in sequenza due diverse formule risolutive, per esempio in una forma:
(A X A' X') (B Y B' Y') .

Y Perm: F (R U') R' (U' R) (U R') (F' R) (U R') U' (R' F) (R F')

Azione: Scambia una coppia di angoli opposti ed una coppia di spigoli adiacenti senza alterarne l'orientamento
Utilizzata nel PLL del Fridrich

La formula si può ottenere concatenando due diffenti formule che realizzano entrambe una T shape (orientamento); le due formule sono:
F (R U') R' (U' R) (U R') F' = (F R U' R') U' (R U R' F') = y' U (F R U' R') U' (R U R' F')
R (U R') U' (R' F) (R F') = (R U R' U') Lw' (U R U' R') Lw
sono entrambe ottenute col commutatore (la seconda già esaminata); dette S e P le sostituzioni e X e Y le sequenze base concatenandole (unendole) realizzano una formula del tipo:
S X S' X' Y P Y' P'

dalla y' U (F R U' R') U' (R U R' F')

Sequenza base: F R U' R'
Sequenza base inversa: R U R' F'

Sostituzione: U [ la U iniziale non viene eseguita; essendo una mossa iniziale sulla Up viene omessa pensando di eseguire un riorientamento y' del cubo e, una volta completata la formula, una U' di riposizionamento ]
Sostituzione Inversa: U'

dalla (R U R' U') Lw' (U R U' R') Lw

Sequenza base: R U R' U'
Sequenza base inversa: U R U' R'

Sostituzione: Lw'
Sostituzione Inversa: Lw

Se si considera la formula unione delle due sopra descritte:
y' U (F R U' R') U' (R U R' F') + (R U R' U') Lw' (U R U' R') Lw

T Perm: R (U R') U' (R' F) (R2 U') R' (U' R) (U R') F'

Azione: Scambia una coppia di angoli adiacenti ed una coppia di spigoli opposti senza alterarne l'orientamento
Utilizzata nel PLL del Fridrich

Si ottiene dalle stesse due fomule considerate precedentemente per la Y perm ma scambiandone l'ordine:
R (U R') U' (R' F) (R F') = (R U R' U') Lw' (U R U' R') Lw
seguita dalla
F (R U') R' (U' R) (U R') F' = (F R U' R') U' (R U R' F') = y' U (F R U' R') U' (R U R' F')

andando a comporre la formula si ottiene:

R (U R') U' (R' F) (R F') + F (R U') R' (U' R) (U R') F' =
(R U R' U') R' (F R F') + (F R U' R') U' (R U R' F') = (R U R' U') Lw' (U R U' R') Lw + (F R U' R') U' (R U R' F') = (R U R' U') Lw' (U R U' R') Lw (F R U' R') U' (R U R' F') = (R U R' U') Lw' U R (U' R' Lw F) R U' R' U' (R U R' F') = (R U R' U') Lw' U R R U' R' U' (R U R' F') = (R U R' U') (R' F R2 U' R' U') (R U R' F')
= R (U R') U' (R' F) (R2 U') R' (U' R) (U R') F'